 |
На предыдущей странице мы убеждаемся, что вариант с одним пересечением достаточно
легкий и допускает несколько решений с различными кросс-суммами. Увеличение количества чисел в строчках и столбцах, а
также сдвиг пересечения не усложняют задачу. Лучше всего, если задача имеет единственное решение, его
и найти труднее и удовлетворение от такой головоломки больше.
Увеличивая количество пересекающихся числовых рядов, мы
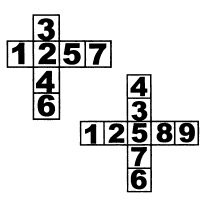
усложняем подобные задачи и уменьшаем количество возможных решений. Для примера рассмотрим пересечение двух строчек
и двух столбцов по 6 клеток, уже более близкое к кроссвордной сетке. Расставить требуется числа от 1
до 20, так чтобы суммы в двух строчках
и двух столбцах были одинаковые.
Четыре числа будут стоять на пересечении и одновременно входить в две суммы.
Следите за методикой решения.
Находим сумму данных чисел:
1+2+3+...+20=210. Она дает при делении
на 4 (2 строки + 2 столбца) остаток 2.
|
 |
Значит и сумма четырех
чисел, стоящих на пересечениях, должна давать при делении
на 4 остаток 2, так как они учитываются дважды. Только тогда
общая сумма будет делиться на 4 и можно определить кросс-
сумму, а затем уже расставить числа. Мы можем поставить в клетках пересечений числа 1, 2, 3, 4, (1+2+3+4=10) и
кросс-сумма получается (210+10)/4=55.
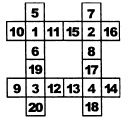
Расставить оставшиеся числа это уже дело
техники, причем снова обращаем внимание на равноудаленные от концов ряда,
они дают одинаковую сумму. Получаем
одно из множества решений.
Увы, снова решение не единственное. В пересечениях можно поставить четверки чисел: (I, 2, 3, 8),(1, 2, 3, 12), (1,
2,3, 16), (1, 2, 3,20) - это не меняя первые три цифры.
|
Можно поменять их, можно переставлять числа в готовом решении. Общий вывод: задача не сильно усложнилась, количество
решений очень большое. Нужно искать другие конфигурации числовых рядов, иные пересечения, чтобы уменьшить количество
решений. Так возникли задания, аналогичные кроссвордам: есть
кросс-сетка, только расставить в ней нужно не слова, а некоторые
числа, чтобы получить требуемый результат. Друг от друга головоломки с кросс-суммами отличаются набором используемых
чисел, исходной фигурой и количеством пересекающихся числовых рядов, но имеют практически одинаковую формулировку:
расставьте числа так, чтобы . Их красота определяется
симметрией расположения, а сложность вообще понятие субъективное. На то они и головоломки, чтобы не иметь общего правила
решения, каждый раз требуется особый подход, новые размышления, но из любой решенной задачи можно и нужно что-то взять
для себя на будущее, если не метод, так хотя бы опыт. Для удобства задачи сгруппированы по исходной фигуре: круги, треугольники, квадраты, многоугольники и т. д. Это позволяет
попытаться выделить, для некоторых групп задач, общие подходы
к решению. Ваша стратегическая цель - это не просто решить задачу, а постараться выделить полезные идеи, интересные методы.
|